Fractal Continuum Mapping Applied to Timoshenko Beams

Resumen

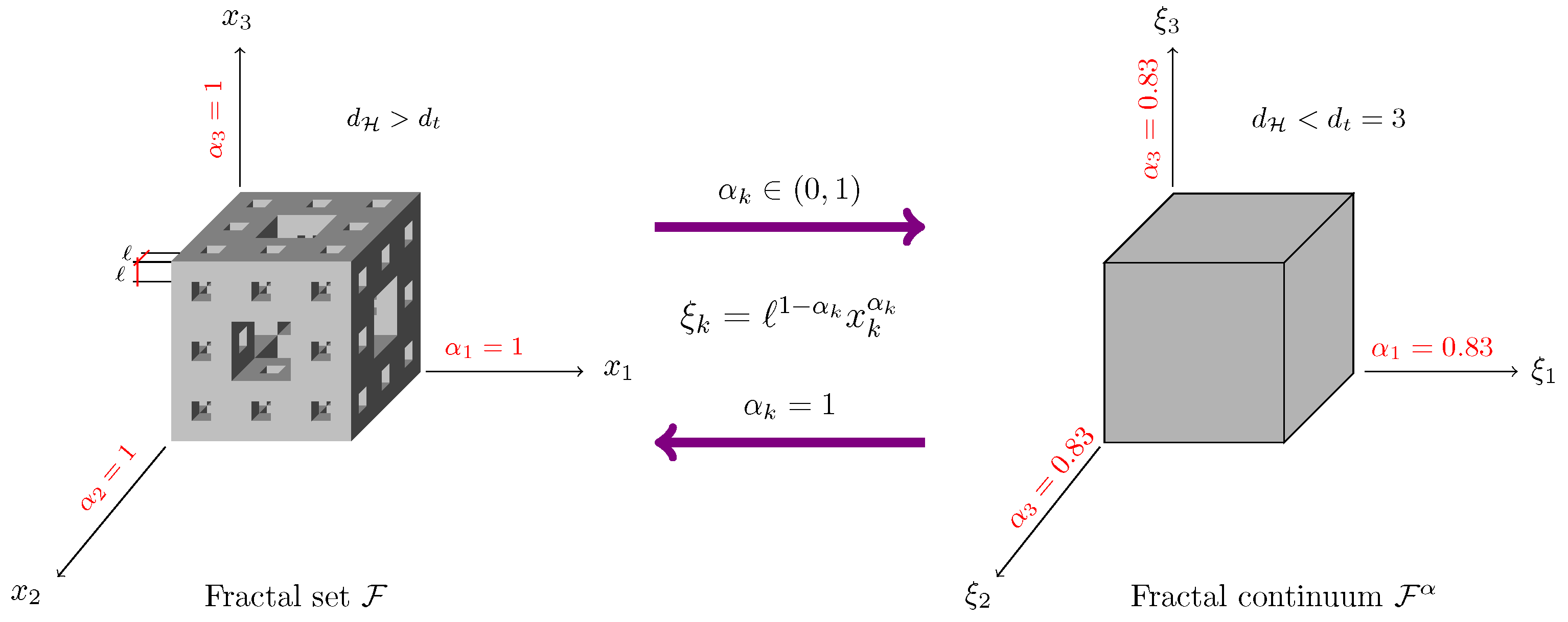
In this work, a generalization of the Timoshenko beam theory is introduced, which is based on fractal continuum calculus. The mapping of the bending problem onto a non-differentiable self-similar beam into a corresponding problem for a fractal continuum is derived using local fractional differential operators. Consequently, the functions defined in the fractal continua beam are differentiable in the ordinary calculus sense. Therefore, the non-conventional local derivatives defined in the fractal continua beam can be expressed in terms of the ordinary derivatives, which are solved theoretically and numerically. Lastly, examples of classical beams with different boundary conditions are shown in order to check some details of the physical phenomenon under study.